Bereichsnavigation
1. Text, diagrams and videos explaining some relevant acoustical rudiments
This Webpage describes the technical abstractions (most of them very familiar to acousticians) that are most relevant to the theory of tempered tunings, and will explain the significance of the numbers in the Webpage describing various theoretical schemes of well-tempered tuning.
Representations of a Vibrating String
If we imagine a taut bit of ideal string clamped at its two ends and producing a musical note – ideal in the sense that it has no stiffness, is absolutely uniform in regard to weight per unit length, and is vibrating just back and forth at 180 degrees (some writers call this a "perfect" string) – we can represent the scope of the vibrations not only in the following fundamental way:

— but also simultaneously in a series of other ways, the first two of which are as follows:
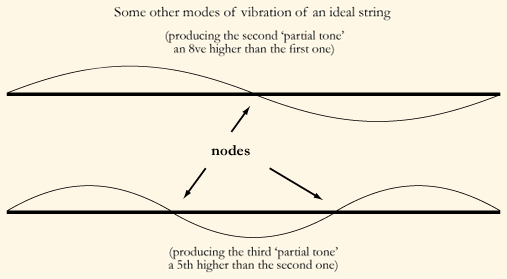
Harmonic Partial Tones
By listening analytically – focusing the ear, as it were, at pitch-levels higher than that of the fundamental – the tuner can distinguish "harmonic overtones" due to these other, simultaneous modes of vibration. The overtones and the fundamental are all called "partial tones", or simply "partials." The second harmonic partial (the first overtone) is an octave higher than the fundamental. (This is because the relevant two parts of the string are each only half as long. The back-and-forth vibrations in this mode are therefore twice as fast; and, vibrations twice as fast yield a pitch an octave higher.) The third harmonic partial is a perfect 5th higher than the second one. (This is because the relevant three parts of the string are each only 2/3 as long as the two parts for the second partial. The vibrations in this mode are therefore 3/2 as fast, and vibrations 3/2 as fast yield a pitch a perfect 5th higher.) And so on for the fourth, fifth, sixth etc. harmonic partials. They tend to become weaker and weaker on the way up. For most keyboard tuning, it suffices to distinguish clearly the first six. (To tune the deep bass notes on a modern piano very well in Equal Temperament, it can be useful to hear their seventh and/or ninth and/or even eleventh partial. But those very low notes are not used in The well-tempered clavier.)
Playing a "harmonic," i.e. a harmonic overtone, on a bowed string instrument is a matter of drawing the bow across the string while touching the string gently with a fingertip – not pressing it down to the fingerboard – at a potential node for a mode of vibration producing one of the overtones. The node for the second partial tone is halfway along the string; the nodes for the third partial tone are 1/3 and 2/3 along the string (either one will do, or both at once); and so on. Here is a video showing how a cello string looks when each of the first two overtones is thus singled out:
Overtones can be singled out on a piano by tapping a high note strongly while holding down the key for a lower note (so that the strings for the low note are not dampened and are thus free to vibrate) which has an overtone at about the same pitch-level as that of the high note. The sound-wave vibrations of the high note will be conveyed not only to our eardrums or to a microphone (via the bridge and soundboard and surrounding air), but also (mainly via the bridge) to the strings which the left hand is keeping undamped; those strings will vibrate "sympathetically" (as it were) in the mode that yields the overtone at the approximate high pitch-level of the right hand's note; and we will hear, isolated, that overtone of the left hand's otherwise unstimulated string. You can hear this in the first seven tracks of the next video (see below).
Differences between Real and "Ideal" Strings
Real strings are not exactly like the ideal ones represented schematically in the diagrams shown above, but the differences are not big enough to affect the theory of tempered tuning.
Organ Diapason Pipes
For physical reasons which are more intricate to explain, and which therefore will not be explained here, one can also distinguish harmonic partials in the notes produced by organ Diapason pipes. (The relevant information is in books on musical acoustics. One of the best such books – and it includes references to the best of the others – is the second edition of Donald E. Hall's Musical Acoustics, Brooks/Cole Publishing Company, Pacific Grove, California, 1991.)
Pure and Impure Consonant Harmonic Intervals
All tuners, and some musicians, distinguish between pure and impure consonant intervals. A pure consonant interval is characterized by an exact match between (a) a not very high harmonic partial tone of the lower of the two notes and (b) the fundamental or a not very high harmonic partial tone of the higher note. In the following musical notations, each black note-head represent a fundamental partial tone, while the diamond-shaped note-heads represent the first five overtones:
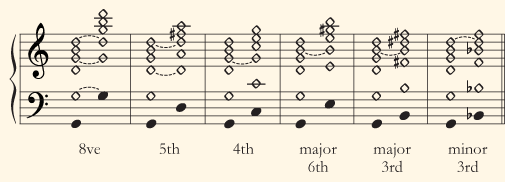
In an impure consonant harmonic interval, the match is slightly inexact.
Orders of Magnitude of (Musical) Intervallic Amounts
Whether the amount of impurity in an impure consonance is sufficient to make the interval sound sour is a psycho-acoustical fact. Here let us borrow from physics the handy concept of "orders of magnitude" based on multiples of ten. If we may say, very approximately, that the order of magnitude of melodic steps in Western music is about one or two tenths of an octave, then we may also say that:
- An impurity on the order of a hundredth of an octave, or somewhat less, is enough to render a consonant interval sour ("out of tune"). Here my equivocation with the phrase "or somewhat less" is due to the fact 5ths and 4ths tolerate less impurity than 3rds and 6ths.
- An impurity of one or just a few thousandths of an octave is perceptible to tuners but is not enough to render a consonant interval sour.
- An impurity of only one or a very few ten-thousandths of an octave is difficult to perceive and even, under certain interesting physical circumstances, impossible to achieve: the interval "draws pure."
The following table is reproduced from Ronald Turner-Smith's and my book Mathematical Models of Musical Scales:

Beating in Impure Harmonic Consonances
If a perceptibly impure harmonic interval is played on a keyboard instrument, one of the two ways in which the impurity is perceived is that a more or less subtle "beating" is heard: a regular throbbing of intensity due to the imperfect unison between partial tones. Because of the imperfection, the two sound-waves of the partial tones periodically reinforce and cancel each other. In the following schematic representations, the horizontal dimension represents time, the vertical dimension intensity:
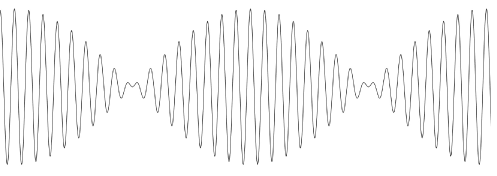
Beats caused by Sympathetic Vibrations
Such beats can be heard in the part of the next video where my right hand taps a high note on the piano briskly but only for an instant while the left hand holds down the keys for two low notes which each happen to have an overtone at about the same pitch-level as that of the high note. Each of the undamped strings (for the low notes) is thus driven to vibrate in the mode that yields the overtone at the approximate pitch-level of the right hand's note. You will hear just those two overtones without the other partial tones of the left hand's unplayed notes. And, the match – the unison – will happen to be imperfect, so those two slightly mismatched overtones will periodically reinforce and interfere with one another: this is (as mentioned above) the meaning in musical acoustics of the terms "beating" and "beats."
"Surging" and "Intermittent" Beating in Equal Temperament
The demonstrations in that next video are done on a piano tuned in Equal Temperament, which has been the normal kind of piano tuning for more than 150 years. The Webpage describing various schemes of "good temperament" will explain more about it. Even without the detailed explanation, however, we can hear on such a piano some psycho-acoustical qualities of beating at various rates.
At less than about once per second, the beating is difficult to distinguish from the way in which the timbre of any single note on the piano changes anyway during a few seconds because the strings are real, not "ideal." When we hear beating at somewhat faster rates, but still no faster than six per second, we can readily distinguish the rise and fall of intensity within each beat. This is called surging. But if the beats are somewhat faster than six per second, they no longer "surge" but instead have an unpleasantly intermittent, "off-and-on" quality. Such is the case in Equal Temperament among the major 3rds and 6ths in the middle of the keyboard. This can be heard in the last two tracks of the following video (my warm thanks to Wolfgang Klatt, a Bösendorfer agent in Berlin, for lending this instrument to the Institute and tuning it.):
At very fast rates, the beating no longer sounds intermittent. It has instead a quality for which the technical term is roughness, but which is really no more unpleasant than the very fast flashing of images on a movie screen.
Genesis of Tempered Tuning
The need for tempered tuning on keyboard instruments with a small number of fixed, i.e. not flexible, pitch-locations in each octave is due to the fact that the sound-wave frequency ratios for consonant harmonic intervals when (a) they are tuned pure (like a car horn or a bagpipe's drone) and (b) the timbre is "harmonic" (i.e. the sound-wave frequency of the second partial-tone is exactly twice that of the fundamental, the sound-wave frequency of the third partial-tone is exactly three times that of the fundamental, and so on) are between small whole numbers: 2:1 for an octave, 3:2 for a perfect 5th, 4:3 for a perfect 4th, 5:4 for a major 3rd, 5:3 for a major 6th, 5:2 for a major 10th; 6:5 for a minor 3rd, and so on. Consider the following three "wrinkles" among certain combinations of such intervals:
(1) The "Lesser Diesis"
A chain of three pure major 3rds – for instance, A♭-C-E-G♯ falls short of a pure octave. Since the frequency-ratio for each such 3rd is 5:4, the ratio for a chain of three in succession is 5:4 x 5:4 x 5:4 = 125:64. This is shy of a pure octave with its frequency-ratio of 2:1 = 128:64. The 128:125 discrepancy is too small to serve as a melodic interval in a normal Western tune, but is nevertheless plenty large enough to render a major 3rd very sour. This is shown in the following video (for which I decided there was no need to demonstrate the "greater diesis," the amount by which the sum of four pure minor 3rds falls short of a pure octave: the lesser diesis is bad enough to make the point!):
(The smallest kind of melodic interval in normal Western music is a "semitone" such as between a 4th and a major 3rd (a "diatonic semitone") or between a major 3rd and a minor 3rd (a "chromatic semitone"). The simplest possible ratio for a diatonic semitone (i.e if the 4th and the major 3rd are each pure) would be 4:3 x 4:5 = 16:15; the simplest possible ratio for a chromatic semitone (i.e. if the major and minor 3rds are pure) would be 5:4 x 5:6 = 25:24. But since 25:24 = 125:120, which is nearly twice as big as 128:125, the interval due to this latter ratio would be more appropriately called a "quarter-tone" than a semitone.)
To demonstrate a use of the Lesser Diesis in chordal harmony, I will use an Italian-style harpsichord equipped with more than 12 notes in each octave:
In the late 16th and early 17th centuries, many Italian keyboard instruments had 13 or 14 notes per octave, for use with a meantone temperament. (Please don’t expect me to explain that term here. It refers to a kind of tempered tuning in which each chromatic note is either a flat or else a sharp but cannot do double duty. Such tuning was used on practically all 16th-century keyboard instruments but is irrelevant to Bach’s music.) This particular harpsichord has 15 notes per octave. I have tuned on it the following web of pure, untempered consonant intervals:

With these pure intervals I can play some phrases making salient use of the chain of pure major 3rds, E♭ - G - B - D♯, and of the resulting quarter-tone between D♯ and E♭:


(In this last example I have tried to make the Lesser Diesis function as a melodic interval. If you still find it not viable as such, your opinion matches the consensus of the mainstream of Western musical culture, inasmuch as musical notation provides normally for semitones but not for quarter-tones.)
(2) The Pythagorean Comma
A melodically zigzag succession of six pure 5ths up and six pure 4ths down for instance: A♭-E♭-B♭-F-C-G-D-A-E-B-F♯-C♯-G♯ exceeds a pure octave. This discrepancy, which is called the "Pythagorean comma," is somewhat more than half as big as the previous one. Its ratio is between rather longer numbers (531441:524288).
(An easy way to think of calculating the frequency-ratio for the Pythagorean Comma is to find first the ratio of the kind of whole-tone that would be gained by going up a pure 5th and then down a pure 4th: 3:2 x 3:4 = 9:8, and then find the ratio of the interval gained by going up a scale of six such whole-tones: 9:8 x 9:8 x 9:8 x 9:8 x 9:8 x 9:8 = a ratio between two long numbers: and then finding the ratio which expresses the difference between that and 2:1.)
A Paradox
Each of the chains of intervals which I have spelled out here begins with a flat and ends with a sharp. But in the chain of three pure major 3rds the sharp is, when considered as a pitch-class (i.e. as a set of notes one or more octaves apart from each other), lower than the flat, whereas in the chain of twelve pure 5ths & 4ths, the sharp is higher than the flat. In the following two illustrative diagrams, the zeros mean that the sets of intervals represented by the pitch-class relations are pure, i.e. there is "zero impurity":

- but G♯ is higher than A♭ in the following chain:
![]()
In each case the way we musicians customarily name the notes helps us accept that there is a difference, but in reality it is a matter of two opposite kinds of difference.
(3) The Syntonic Comma
The third kind of difference to be described here is more difficult to believe in (if one hasn't actually heard it in an acoustical demonstration with pure harmonic consonances) because it is not reflected in the way the notes are written and named:

That is, a melodically zigzag chain of two pure 5ths up and two pure 4ths down yields a major 3rd which is larger than pure, as demonstrated in Track 2 of the video showing some chains of pure intervals being tuned on a piano. This discrepancy is called the "syntonic comma." Its frequency ratio could be calculated as follows by a school-child (or at least one who enjoys arithmetic):
While the string producing a C vibrates 64 times (during some fraction of a second), which happens to be 4 x 16, the string for the E above it that is pure in relation to it vibrates 5/4 x 64 = 5 x 16 = 80 times.
Meanwhile, the string for the G a pure 4th below that same C vibrates 3/4 x 64 = 3 x 16 = 48 times.
Since 48 = 2 x 24, the string for the D a pure 5th above that G (at 48) vibrates 3/2 x 48 = 3 x 24 = 72 times.
Since 72 = 4 x 18, the string for the A a pure 4th below that D (at 72) vibrates 3/4 x 72 = 3 x 18 = 54 times.
Since 54 = 2 x 27, the string for the E a pure 5th above that A (at 54) vibrates 3/2 x 54 = 3 x 27 = 81 times.
So, the ratio for the syntonic comma is 81:80.
(In a simpler way of writing the same calculation – namely 3^4:(5x2^4) = 81:(5x16) = 81:80 – the fourth power of 3 is involved because the complex of intervals includes four pure 5ths/4ths, for each of which 3 is the operative prime number; the number 5 is involved because the complex of intervals includes a pure major 3rd, for which 5 is the operative prime number; and a power of 2 is included to provide the necessary octave-adjustments.)
In the following video, some chains of pure 5ths & 4ths are tuned on a piano to demonstrate the Syntonic and Pythagorean commas:
In the following video, I play on the Italian-style harpsichord the pure E♭-major triad which we had before on that instrument, and then the pure 4ths & 5ths, E♭ - B♭ - F - C (which we also had); and then, after hearing that the G is thus a comma lower than pure in relation to C, I raise it and carry on with tuning a chain of pure 4ths & 5ths until reaching middle D♯ which will now be not only a comma higher than a pure octave above the low E♭ that I started from, but also a hefty quarter-tone high in relation to the low D♯ that we had previously had as part of the pure chain, E♭ - G - B - D♯:

That hefty quarter-tone, equal to the sum of the Lesser Diesis and the Pythagorean Comma, is called the "Greater Diesis." (Both of the notes involved in it are notated as sharps (in this case D#) because we have only two ways - sharp and flat - of designating a black-key note on the keyboard. Our notation switches from flat to sharp for the enharmonic difference of the Lesser Diesis, and here we switch again for the Pythagorean Comma, but this means, perforce, switching back to a sharp in our notation.)
A Unit of Measure – the "Schisma" – for Specifying Amounts of Desired Impurity
The theoretical "melodic interval" – i.e. the quasi-melodic size – of the syntonic comma happens to be almost exactly 11/12 that of the Pythagorean comma (the fraction theoretically a thousand times more precise would be 11.008/12.008); and, the size of the lesser diesis – the first of the "wrinkles" described above, the amount by which pure major 3rds don't add up to a pure octave – happens to be almost exactly 21/12 that of the Pythagorean comma. The traditional name for the difference between the syntonic and Pythagorean commas is "the schisma." So, in the Webpage describing various theoretical schemes of well-tempered tuning I will use the schisma as the unit of measure for tempering, since it conveniently happens to be for all practical purposes the same as 1/11 of the syntonic comma, 1/12 of the Pythagorean comma, and 1/21 of the lesser diesis. It amounts to about one percent of a whole-tone. (I can't say exactly what the percentage is, because the whole-tones are of slightly different sizes in different kinds of tuning.) The octave always amounts to the sum of five whole-tones plus two "diatonic semitones," i.e. semitones between notes with different note-names (such as D-E♭, E-F and F♯-G).
Several 18th-century German theorists of tempered tuning used 1/12 of the Pythagorean comma as their unit of measure for tempering.
A Quick Rule of Thumb for Calculating a Desired Rate of Beating
To convert from an amount of impurity to the resulting rate of beating, one has to take account of the pitch level of the lowest impure unison between partial tones of the two notes forming the interval. It can be done quickly if the unit of measure for impurity is the schisma. There are two steps to understanding this rule of thumb:
1. Suppose that a keyboard instrument tuned at modern concert pitch, i.e. with "concert A" at 440 HZ, a certain harmonic interval is consonant because of a unison between partial tones at about 880 HZ (i.e. an octave higher than concert-A at 440). If it is impure by a syntonic comma due to the fact that one of those partial tones is exactly at 880 HZ but the other one is higher by a syntonic comma, i.e. is exactly at 81/80 of 880 HZ, then the difference in HZ between those two partial tones will be 1/80 of 880, which happens to be 11, which in turn happens to be the same as the number of schismas in the syntonic comma. So, at modern concert pitch, the number of beats per second due an imperfect unison between partial tones at the pitch-level of soprano's high A is the same as the amount of impurity measured in schismas.
2. Knowing this, you can readily calculate as follows the approximate rate of desired beating for impure consonances whose lowest unison is somewhere other than soprano's high A at modern concert pitch:
- If it is at alto's high D, then the rate should be 2/3 the number of schismas.
- If it is at operatic soprano's high D, the rate should be 4/3 the number of schismas.
- If it is at the violin's open-string E, the rate should be 3/4 the number of schismas.
- If it is an octave higher than that, the rate should be 3/2 the number of schismas.
- If it is at soprano's high C♯ , the rate should be 5/4 the number of schismas.
And so on. If you haven't developed a "feel" for judging different rates of beating, you can set a metronome at the desired rate and proceed from there. You must of course multiply by 60 the numbers of beats per second in order to get the equivalent metronome-settings, which are for numbers per minute. (If you are tuning at a lower concert-pitch level, divide your HZ-number for concert A by 440 and multiply by the resulting amount.) If for instance you wanted to tune a certain interval to beat exactly seven times per second, the number per minute would be 7 x 60 = 420, and so you could set the metronome at 105 and then make the interval beat exactly four times per click or flash of the metronome.
The Sense of Melodic Distortion in Impure Consonances
I said that beating is one of two ways in which impurity in a consonant harmonic interval is perceived. The other way – by melodic nuance – cannot be measured by a clock or metronome, and is therefore less useful to the tuner, but in musical performances it can often be even more important than the qualitative aspects of the beating of tempered consonant harmonic intervals. Acoustic beats can be subtle and can get "lost" when one hears the performance from a distance (instead of in an intimate setting such as that of Bach playing The well-tempered clavier for one or two students), whereas melodic distortions on a harpsichord or piano may readily "carry" throughout a moderate-size auditorium.
Using a Different Unit of Measure – the "Cent" – for Semitones
There is no natural sense of purity vs impurity in regard to dissonant intervals such as semitones. However, the fact that everyday musical terminology distinguishes between whole-tones and semitones but not between various sizes of whole-tone or semitone shows that we like to think of each of these two kinds of melodic step as being more-or-less uniform. In equal temperament, which everyone who has heard a lot of modern Western music is very familiar with, the octave is divided into twelve exactly equal semitones; so, the commonly used unit of measure for the musical intervals in any scale (regardless of how it is tuned) is the "cent," which is one percent of one twelfth of a pure octave. My diagrams for various kinds of tempered tuning will show in schismas how much the various 5ths and major 3rds are to be tuned impure, but in cents the sizes of the twelve semitones and the most subtle differences in size amongst them.
The Pythagorean comma amounts to some 23.46 cents, 1/12 of which thus amounts to some 1.955 cents. The schisma amounts to some 1.954 cents. If you prefer clumsy long numbers to simple short ones, you may convert into cents my reckonings in terms of schismas in the next Webpage.

