Bereichsnavigation
6. The French Background
Early 18th-century French keyboard tuning practices form a significant part of the historical background to Bach's concept of a well tempered organ or harpsichord. He is known to have been influenced, early in his career as a composer (in the first few years of the century) by contemporary French-style music in general and by French organ music in particular. And, it is very likely that when he visited Hamburg in 1720 to audition for the position of organist at an important church there, he met Johann Mattheson, who lived in Hamburg and who later wrote a delightfully sharp of account of the fact that Bach, though by far the best organist to apply for the position, was not hired. The presumed acquaintance between the two musicians is significant because Mattheson wrote and published in 1720 a booklet commenting with approval upon an article, in a recent issue (1718) of a French cultural journal, which said that nuances of keyboard tuning were the reason why modern composers would often favor the "transposed modes," i.e. keys not corresponding to the traditional church modes: keys such as C and B major and minor (as distinct from old-fashioned keys like D minor, which was equivalent to the traditional Dorian mode). The earliest extant versions of pieces in Das wohl temperirte Clavier were written by Bach, soon after returning home from Hamburg, in a notebook for his eldest son.
A comprehensive account of 17th- and 18th century French styles of keyboard tuning is available in my article,Innovations in temperament and harmony in French harpsichord music, published in the journal, Early Music (2013/41: 403-420). This article includes detailed discussion, illustrated by musical examples from twelve compositions, of the significance of those historical kinds of tuning in relation to the development of harmonic style in French harpsichord music. Here are incipits of the twelve pieces.
Jacques Champion de Chambonnières, a Rondeau in F major:
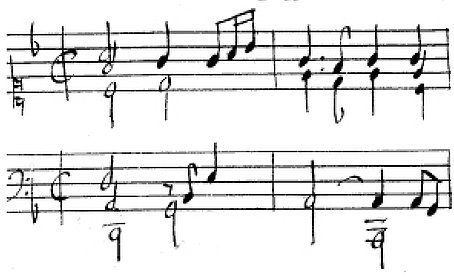
– and a Pavane and Gigue in G minor:
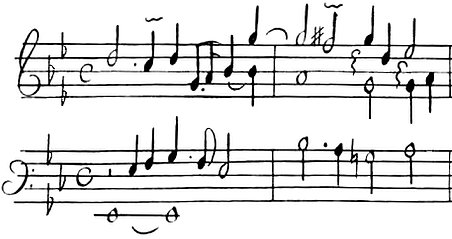
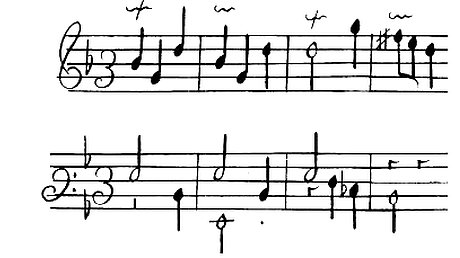
Louis Couperin, a long Passacaille in G-minor:

– and Chaconnes in G and C minor:


– and a Pavane in F♯ minor:
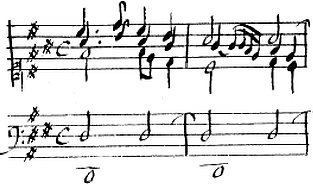
François Couperin, the prelude in A major from L’Art de toucher le clavecin:

and a Courante and Sarabande in D-minor from the Premier livre de pièces de clavecin:

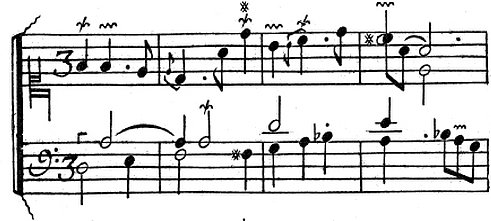
Jean-Henri D’Anglebert, a Sarabande in D minor[1]:

Jean-Philippe Rameau, "L’Enharmonique" (in G minor):
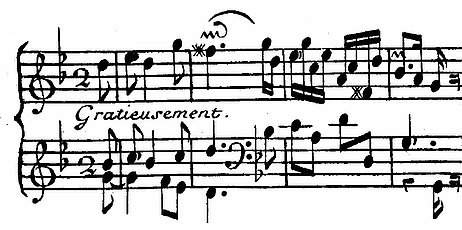
The discussions of these examples are based on demonstrations in which each example has been performed in two different temperaments. We intend to make recordings of these examples available on the web within a year or so.
The article in Early Music will include English translations of relevant passages from ten French writers of the 17th and 18th centuries. That set of French citations was initially published and discussed, in German, in my Stimmung und Temperatur; here is an English translation of that earlier discussion (incorporating but not translating the material cited from the French sources):
In three papers published in 1701, 1707 and 1711 in the Mémoires of the French Royal Academy of Sciences, Joseph Sauveur investigated various equal divisions of the octave. In the first paper, he proposed to quantify musical intervals in terms of a unit of measure amounting to 1/301-octave, which he called (for reasons which I needn't bother to explain here) the "eptaméride." (Since log 2 = 0.3010, one could readily determine the number of eptamérides in an interval with a given pitch-frequency ratio by (a) converting the ratio to a decimal number and (b) looking up that number in a log table.)[2] In the second paper, entitled Méthode générale pour former les systèmes tempérés de musique, et du choix de celui qu’on doit suivre, he started from the premise that "les système diatonique," i.e. the diatonic scale, would, if untempered, contain three whole-tones with the pitch-frequency ratio 9:8 (= 3/2 x 3/4), two slightly smaller whole-tones with the ratio 10:9 (= 5/4 x 8/9) and two semitones with the ratio 16:15 (= 4/3 x 4/5):
"mais pour rendre tempéré ce système, au lieu des tons majeurs et mineurs il faut prendre un ton moyen; alors l’octave sera composée de 5 tons et de 2 semitons."[3]
He then worked out a rule to the effect that in a regular tempered scale, the unequal semitones (i.e. the diatonic vs chromatic semitones) should be no more alike in size than they are in a major whole tone (9:8) in just intonation, nor more disparate than they are in a minor one (10:9); he said that to avoid an excessively fine division of the scale, the sizes of the two kinds of semitone should be exact multiples of the difference in size between them; and he showed that the 31-, 43- and 55-divisions are the only ones which fit these specifications. It so happens that they approximate closely to 1/4-, 1/5- and 1/6-comma Meantone Temperament respectively. (All three of them contain satisfactory perfect 5ths. In the 31-division, the diatonic semitone amounts to 3 units and the chromatic one to 2; the whole-tone thus consists of 5; the octave contains 5 x 5 + 2 x 3 = 31 parts; and 10/31-octave happens to make a virtually pure major 3rd. In the 43-division, the diatonic semitone amounts to 4 units and the chromatic one of 3; the whole-tone thus consists of 7; the octave contains 5 x 7 + 2 x 4 = 43 parts; and 14/43-octave makes a major 3rd practically the same as one tempered larger than pure by 1/5-comma. In the 55-division, the diatonic semitone consists of 5 units and the chromatic one of 4; etc.) He decided to consider Equal Temperament as well, "parce qu’étant fort simple il a eu ses partisans." It remained to choose among the four resulting systems. He remarked that although Equal Temperament "a son usage chez les joueurs d’instruments moins habiles à cause de sa simplicité," nevertheless "les habiles joueurs l’ont rejeté" because of its impurity. The 55-division was, he said, "celui dont les musiciens ordinaires se servent" (it corresponds approximately to 1/6-comma Meantone); but he nevertheless favoured the 43-division and not only for such non-musical reasons as its nice relation to the common log table and the fact that its whole tone is "un milieu arithmétique entre les 3 tons majeurs et les 2 mineurs," but also for some musical reasons:
"L’usage montre dans la musique que des consonances ... également alterées ne choquent pas tant l’oreille que des consonances plus alterées melées avec d’autres plus justes, et ... dans ce système de 43 la tierce majeure ... (et) les quintes ... ont pour différence 1 eptaméride (i.e. about 1/5 comma).... La tierce mineure et la sexte majeure ont à la verité 2 1/6 d’eptaméride de différence: mais l’expérience montre qu’une grande différence est plus supportable dans les consonances, dont le rapport est exprimé par de grands nombres, comme dans la tierce mineure qui est de 56, que dans les intervalles dont les rapports sont exprimés par des petits nombres, comme dans la quinte qui est de 2 à 3."
The secretary of the Academy, Bernard de Fontanelle, commented apropos:
"C’est par cette raison que les facteurs d’orgues et de clavecins suivent le système de M. Sauveur, et non celui des musiciens ordinaires."
Confirmation of this latter assertion can be found (a) in the fact that Etienne Loulié in hisNouveau système de musique (1698) described 1/4- and 1/5-comma meantone and said that the latter temperament was "plus en usage qu’aucun autre," and (b) in an account, in Sauveur’s next article (1710), of contemporary harpsichord tuning:
"Le système de 43 est un moyen entres les systèmes extrèmes légitimes.... Les facteurs de clavecins du roi et de Paris, qui ont monté l’octave de leurs clavecins sur mon monocorde, dont l’octave est divisée en 43 mérides, on trouve leur tempérament fort juste; et j’ai divisé l’octave d’un monocorde en 31, 45 (sic), 50 et 55 parties, mettant la corde du monocorde à l’unison avec un C sol ut du clavecin qu’on avoit accordé très exactement; on a ensuite placé le chevalet sous la corde, en la mettant à l’unisson avec chaque touche du clavecin; on a trouvé que le chevalet se recontrait toujours sur les divisions du système de 43 ou, à très peu pres, et s’éloignoit des divisions des autres systèmes, lorsqu’elles étaient fort différentes de celle du système 43."
Sauveur's account of harpsichord tuning concluded, however, with the following remarks:
"Je sais qu’il y a des facteurs qui montent leur clavecins avec des accords plus piquants, et par consequent peut-être plus approchants des autres divisions."
Had these more piquant notes disrupted the tempering of the diatonic C-major scale, it would probably have been impossible for Sauveur, who measured the intervals from C, to detect that there were only a few of them. And, evidence from another relevant documentary source, i.e. the brief "méthode d’accorder le clavecin" appended to Lambert Chaumont’s Pièces d’orgue (1695), suggests that the irregular notes were B♭ and E♭. According to this method, one should tune most of the 5ths
"dans un certain tempérament entre le juste et le faible accordé ... éprouvant toujours par la tierce si l’opération est bonne."
(Nothing more is said about the 3rds; they were to be "good," yet there is no statement specifying that they were to be "pure" in the modern sense of this English word as a technical term meaning "not tempered.")
But B♭-F and then E♭-B♭ were to be tuned either "forte" or "faible" and whichever alternative we regard as the irregular one will render B♭ and, a fortiori, E♭ more heavily tempered in relation to G than are B and E.
The practice of tuning B♭-F and E♭-B♭ larger than pure had presumably been due originally to an ambiguity in a set of tuning instructions, in Mersenne’s renowned Harmonie universelle (1636), for 1/4-comma meantone temperament. The first part of the instructions covered the chain of tempered 5ths among the naturals (F, C, G, D, A, E, B), starting from F. Mersenne said that C, G, D, A, E and B should each be tuned "foible" (i.e. "faible"), meaning "lower than pure." Going on then from B, he said that B-F♯-C♯-G♯ were to be treated the same way. Then he went back (as it were) to F and said that its lower 5th should be tempered "forte"; and he said the same thing about the 5th below that note. Of course he meant that each of those two notes, B♭ and E♭, should be tuned higher than pure in order to obtain a intervals of a 5th, namely B♭-F and E♭-B♭, smaller than pure. But some people evidently misunderstood, and he corrected the misunderstanding in an appendix. The page containing the entire set of instructions remained unchanged, however.
Jean-Philippe Rameau in a section on temperament in his Nouveau système de musique théorique (1726) said that to "pouvoir établir un tempérament qui ne souffre aucune difficulté" (the phrase "établir un tempérament" here meant "to provide a correct theoretical account of the matter," since he had already remarked that keyboard musicians tempered their instruments "même assez régulièrement" i.e. fairly consistently "sans autre secours que celui de l’oreille"), "nous devons avoir égard à trois choses: à l'expérience des cordes, aux raisons marquées par les nombres, et à l'habitude où l’on est d’accorder les clavecins." By the third and most pragmatic of these criteria he knew that "on est dans l'habitude d’y affaiblir un tant soit peu les premières quintes" in order to have a "tierce majeure dans la justesse que demande l’oreille"; and by a circular argument involving exclusively the other two criteria he arrived at the conclusion that "il n’a qu’à diminuer chaque quinte de quart de ce comma" (the syntonic comma; in 1737 he would merely say that the actual amount was "à peu près d’un quart de comma"). The argument was as follows: "L’expérience des cordes nous apprend que la quinte frémit toujours, quoiqu’un peu diminuée de sa justesse; et que la tierce majeure ne frémit plus, si peu qu’on l’altère;" therefore we know from "les nombres," that "la tierce majeure juste avec Ut" on keyboard instruments must have the ratio 5:4, and hence the 5ths making a chain between C and E (i.e. C-G-D-A-E) must be tempered by 1/4 comma. The vagueness of the concept "frémir" seems to be the most vulnerable point in this argument, which Rameau discarded in his next book and which is contrary to the testimony of Loulié, Sauveur and a host of other 18th-century writers on tempered tuning.
Rameau went on to say that "Lorsqu’on est arrivé au milieu de la partition, on rend les quintes un peu plus justes, et cela de plus en plus jusqu’à la dernière." He hesitated for a moment to specify exactly where this process should begin: although "on ne peut se dispenser de rendre les quintes plus justes depuis ce Sol# jusqu’à la fin", nevertheless
"Il ne faut pas attendre qu’on soit arrivé au Sol# pour rendre les quintes un peu plus justes, et l’on doit s’y prendre dès la quinte d’Ut# à Sol# (supposé qu’on ait commencé la partition par Ut) ... et par ce moyen les dernières tierces majeures ... souffrent beaucoup moins; quoi-qu’on ne puisse dispenser de les rendre pour lors un peu trop fortes, non plus que les deux dernières quintes."
Having thus arrived at an account mentioning all twelve of the notes, he made an adjustment which shows that he was aware of its defects without being quite capable of the quantitative subtlety necessary to get it right:
"Pour que les intervalles conservent toute la justesse possible dans les modulations les plus usitées, il faut commencer la partition par Si B-mol, et ne rendre ... les quintes un peu plus justes, que depuis Si à Fa#."
Had he not said that each and every irregular 5th must be larger than the preceding one, he could readily have admitted one more of them and thereby got E♭-B♭-F to be the ones that were "trop fortes" while still enabling B-F♯ to be, as he evidently wanted it to be, larger than the diatonic 5ths.
At his moment of apparent indecision as to whether the tuning started on C or B♭, Rameau made a sure-footed assessment of its significance to a creative musician:
"L’excès des deux dernières quintes et des quatre ou cinq dernières tierces majeures est tolérable, non seulement parce qu’il est presque insensible, mais encore parce qu’il se trouve dans des modulations peu usitées; excepté qu’on ne les choisisse exprès pour rendre l'expression plus dure, etc. Car il est bon de remarquer que nous recevons des impressions différentes des intervalles, à proportion de leur différente altération: par exemple, la tierce majeure qui nous excite naturellement à la joie, selon ce que nous en éprouvons, nous imprime jusqu’à des idées de fureur, lors qu’elle est trop forte, et la tierce mineure qui nous porte naturellement à la douceur et à la tendresse, nous attriste lors qu’elle est trop faible. Les habiles musiciens savent profiter à propos de ces différents effets des intervalles, et font valoir par l’expression qu’ils en tirent, l’altération qu’on pourrait y condamner."
In 1752 the science editor of the Encyclopédie, Jean le Rond d’Alembert, in his own description of the tempérament ordinaire (in his Elémens de musique théorique et pratique suivant les principes de M. Rameau), smoothed over the rough spots in Rameau’s account by not associating the ratio 5:4 with the term "tierce majeure juste" and by not saying how large any of the 5ths should be except to specify that C-G-D-A-E were the smallest, B-F♯-C♯-G♯ still smaller than pure, and A♭-E♭-B♭-F "reinforced," and perhaps F-C as well:
"On commence par l’ut du milieu du clavier, et on affaiblit les quatres premières quintes Sol, Ré, La, Mi, jusqu’à ce que mi fasse la tierce majeure juste avec ut; partant ensuite de ce mi, on accorde les quintes Si, Fa#, Ut#, Sol#, mais en les affaiblissant moins que les premières, de manière que sol# fasse à peu pres la tierce majeure juste avec mi. Quand on est arrivé au sol#, on s’arrête; on reprend le premier ut, on accorde sa quinte fa en descendant, puis la quinte Sib, etc., et on renforce un peu toutes ces quintes jusqu’à ce qu’on soit arrivé au Lab, qui doit etre le même que le Sol# déja accordé."
He said that "il y a cinq ou six modes insupportables," and this point, by implying that some of the 3rds were grotesquely large, confirms that at least one of the 5ths (perforce somewhere among the chain A♭-E♭-B♭-F-C) must have been larger than pure.
These tuning instructions give a particular meaning to the discussion of "transposed modes" in the section on music in Jacques Ozanam’s Dictionaire mathématique (1691). Ozanam distinguished between "les modes naturels au naturel" (C-major, D- and E-minor, F-major, G-major and minor, A-minor, B♭-major and B-minor), "Les modes naturels par les chromatiques" (C-minor, D- and E-major, F- minor, A-major, B♭-minor and B-major), and "les modes transposez" (C♯-, E♭-, F♯- and G♯-major and minor). The latter were almost never used, he said, because:
"Quelque précaution que nous prenions en accordant nos instruments pour en rendre tous les accords égaux, il ne laisse pas de s’y trouver toujours quelque inégalité: et c’est ce qui fait que nous remarquons un je-ne-sais-quoi de triste ou de gai, de mélodieux ou de dur, qui nous fait distinguer un mode d’avec l’autre par le secours de l’oreille."
Even without the tuning instructions to inform us that the inequality in question was of a certain more-or-less consistent form, we might infer as much from Ozanam’s statement that it enabled people to recognize the various keys by ear. In the mid-1690s Marc Antoine Charpentier distinguished clearly between two quite different reasons for les transpositions des modes:
"La première et moindre raison, c’est pour rendre le même pièce de musique chantable par toute sorte de voix. La seconde et principale raison, c’est pour l’expression des différentes passions, à quoi la différente energie des modes."
And he made a list, entitled "Energie des Modes", which includes the following characterizations:
D-minor: grave et dévot
G-minor: sérieux et magnifique
C-minor: obscur et triste
F-minor: obscur et plaintif
B♭-minor: obscur et terrible
E♭- minor: horrible, affreux
Charles Masson in the first edition (1697) of his Nouveau traité des règles de la composition did not admit B♭- or E♭-minor, but characterized the others shown above as follows:
D-minor: je-ne-sais-quoi de grave mêlé de gaieté
G-minor: plein de douceur et de tendresse
C-minor: propre pour des sujets plaintifs
F-minor: triste et lugubre
When Ozanam described how unequal temperament made the various keys sound different, he rightly observed that "d’autres circonstances y contribuent aussi come la propriété des instruments"; and Charpentier and Masson (and their later German counterparts such as Mattheson) were influenced, particularly in their characterization of the traditional modes, by ideas that had nothing to do with fine shades of tuning. Yet anyone who has listened attentively to the particular kind of temperament in question (in which B♭, E♭, A♭ and D♭ each make successively darker 3rds and smaller semitones with the next lower diatonic note) will recognize its influence upon the successively darker labels selected by Charpentier and Masson for the less traditional minor keys as they involve more flats. One can see the same kind of influence in Charpentier’s labels for the major keys involving more than three sharps: while G-major was "doucement joyeux", D-major "joyeux et très guerrier" (I do not attribute this label to the influence of the tempered tuning) and A-major "joyeux et champêtre", E-major "querelleux et criard", and B-major "dur et plaintif". The label for E-major is due not only, I believe, to the fact that D♯ was tuned even higher than a leading tone in Equal Temperament, but also to the fact that middle G♯ was tempered high enough to beat intermittently with middle E and with the B next to middle C.
An anonymous article published in 1718 in theMémoires de Trevoux (the remarkably successful Jesuit cultural journal which Voltaire later made such good fun of in a fictional account of the "sickness, confession, death and apparition" of its mid-century editor, Guillaume-François Berthier) undertook to explain "pourquoi l’on emploie quelquefois, dans la composition, les tons ou modes transposés préférablement aux tons ou modes naturels." The author’s grasp of acoustics was so weak that, perhaps taking a cue from Ozanam, he revived in a new guise an ancient Greek precept (going back to Archytus) that musical intervals with superparticular ratios (i.e. ratios answering to the formula n+1 : n for instance, 2:1, 3:2, 4:3, 5:4, 6:5 ... 9:8, 10:9 etc.) cannot be divided into equal parts:
"L’octave, comme on sait, est partagée en douze demi tons; mais ce partage ... ne se peut faire si juste, que ces intervalles particuliers soyent très-exactement égaux entre eux; cette impossibilité ... se rencontre dans la pratique (car dans la spéculation les mathématiciens y réussissent à merveille)"
; but it seems legitimate to infer, from his failure to mention or imply the presence of a wolf 5th, that the tuning under discussion was irregular. He said:
"s’il n’y avait point d’autre différence entre les tons transposés et les naturels, que d’être exécutés ou plus haut ou plus bas, ... il n’y aurait qu’à jouer un air sur un instrument monté ou plus haut ou plus bas, pour produire tout l’effet de la transposition; et c’est néanmoins ce qui n’arrive point. Chacun en peut faire l’expérience, comme je l’ai faite chez un ... de nos plus habiles maîtres; je fis éxécuter sur le même clavecin, une piece en C sol ut naturel; et la faisant jouer ensuite un demi ton plus haut en C sol ut dièse, tous les auditeurs s’aperçurent, qu’il y avait une différence très grande et très sensible: au lieu que cette différence ne se retrouve nullement en faisant jouer la même piece sur deux clavecins, dont l’un serait monté un demi ton plus haut que l'autre.... Aussi le commun des gens, de ceux mêmes qui se plaisent à la musique, ne distinguent-ils pas toujours l’effet d’une piece jouée sur un ton transposé, ou sur un ton naturel les connaisseurs le distinguent très bien, et c’est cette différence dont je dis qu’il est impossible de trouver le fondement, que dans le partage inégal des tons ou intervalles sur les instruments: de là vient aussi que ceux qui ont un grand usage des instruments prétendent que certains tons sont plus gracieux, ou plus doux, plus vifs, ou plus hardis que d’autres. II pourrait bien à la verité se mêler un peu d’arbitraire, dans cette différence de caractères prétendus des tons; mais il est certain qu’il s’y en rencontre quelqu’une. Ainsi en général les tons naturels font une musique plus unie et plus simple, parce que leur partage est le plus exact qui ait pu se faire dans la pratique. Au contraire, les tons transposés sont plus singuliers et plus étranges, le partage de leurs intervalles étant un peu moins juste; mais c’est ce defaut même de justesse exacte, qui en fait l’agrément: cette petite bizarrerie tirant l’âme par là, d’un sentiment trop commun et trop uniforme, réveille son attention, et lui donne une pointe de plaisir. C’est à peu près de ce qui arrive dans les ragoûts: on y met plus de vinaigre, de poivre, et d’autres épiceries, qu’il ne faudrait dans un assaisonnement ordinaire, et le plus convenable à la santé."
Rameau said, in his treatise of 1737 (Génération harmonique):
"Celui qui croit que les différentes impressions qu’il reçoit des différences qu’occasionne le tempérament en usage dans chaque mode transposé, lui élevent le génie, et le portent à plus de variété, me permettra de lui dire qu’il se trompe. Le goût de variété se prend dans l'entrelacement des modes, et nullement dans l’altération des intervalles, qui ne peut que déplaire à l’oreille, et la distraire par conséquent de ses fonctions."
Also discarded (as one might expect) was the doctrine that 5ths could be tempered with greater impunity than 3rds:
"Accoutumez-vous au nouveau tempérament.... L’excès des tierces majeures vous y choquera moins avec le temps, que la diminution des quintes dans le vôtre: d’ailleurs, sur quoi doit tomber la correction si ce n’est sur ce qu’il y a de moins parfait?" And again: "C’est principalement sur la succession fondamentale de ces quintes que l’oreille se guide. ...Qu’importe, après cela, que les tierces, les sixtes, les tons, les demi-tons soient plus ou moins alterés...: tous ces intervalles ne sont que passagers."
Jean-Jacques Rousseau’s response (in the Encyclopédie and again in his Dictionnaire de musique) included the following: "M. Rameau ... dit en vain ... que la variété se trouve dans l’entrelacement des modes ou dans les divers degrés des toniques, et nullement dans l’altération des intervalles; le musicien repond que l'un n’exclut pas l’autre." He had held a grudge ever since Rameau, on behalf of the Academie, had rejected for publication the Dissertation sur la musique moderne with which Rousseau had initially hoped, in 1743, to establish his reputation as a musically creative person (and therefore a philosopher of genius). In that essay itself, however, i.e. before he felt a vested interest in opposing Rameau, Rousseau had observed:
"C’est un fait d’expérience, que les différents tons de la musique ont tous certain caractere qui leur est propre, et qui les distingue chacun en particulier. L’A mi la. majeur, par exemple, est brillant; l’F ut fa est majestueux; le Si bémol majeur est tragique; le Fa mineur est triste; l’Ut mineur est tendre.... Or, si le rapport d’un ut à un sol, ou d’un ré à un la, est le même dans tous les tons, pourquoi produit-il différents effets? [Because in reality] ces rapports ont entre eux de légères différences.... Comparons, par exemple, le C sol ut mineur et le D la ré.... On trouve ... par l’accord ordinaire du clavecin, le demi-ton compris entre le sol naturel et le la bémol un peu plus petit que celui qui est entre le la et le si bémol. Or, plus les deux sons qui forment un demi-ton se rapprochent, et plus le passage est tendre et touchant; c’est l’expérience qui nous l’apprend, et c’est, je crois, la véritable raison pour laquelle le mode mineur du G sol ut nous attendrit plus que celui du D la ré. Que si cependant la diminution vient jusqu’à causer de l’altération à l’harmonie, et jeter de la dureté dans le chant, alors le sentiment se change en tristesse, et c’est l’effet que nous éprouvons dans l’F ut fa mineur.... La mécanique du tempérament introduit dans la modulation des tons si durs, par exemple le ré et le sol dièses, qu’ils ne sont pas supportables à l’oreille."
[2] In the late 19th century this unit of measure was renamed the "savart." Sauveur described in the same paper how he had calculated the pitch frequency of A (in the lowest octave of a baritone’s tessitura) at 100 per second. After tuning a set of organ pipes make pure F-major and minor chords, i.e. with A and A♭ in the ratio 25:24 (= 5/6 x 5/4), he clocked the beating between those two notes at 4 per second, and thus obtained 100 (= 4 x 25) for A. Later he obtained 102 from a more exact measurement, and proposed middle C♯ at 256 as a pitch standard since that is just 1 more than 255 (the frequency for the note a pure major 10th above A at 102, as 5/2 x 102 = 255).
[3] It is quite obvious that Sauveur had taken this premise, albeit without acknowledgment, from a book by Joseph Zaragossa, Fabrica, y uso de varios instrumentos mathemáticos, published in 1674 and dedicated to Zaragossa’s pupil (in mathematics and engineering), Carlos II of Spain.

